Publications
Hermitian and Non-Hermitian quantum optics in integrated optical waveguides
The paraxial wave Helmholtz equation describing the propagation of classical electromagnetic waves close to the optical axis is formally equivalent to the Schrödinger equation of quantum mechanics in two spatial dimensions. This concept has long been exploited to emulate certain aspects of quantum physics using light confined in waveguides, where the refractive index contrast plays the role of the potential in the Schrödinger equation. This has become even more interesting as a complex refractive index material allow to emulate non-Hermitian evolutions.
Our aim is to elevate this correspondence between classical electromagnetism and the Schrödinger equation to the realm of quantum optics, where we showed a straightforward translation of concepts of PT-symmetric evolution with loss and gain not to be possible [1]. However, we could show the first Hong-Ou-Mandel quantum interference of photons in a passive PT-symmetric setting [2]. In order to efficiently model the quantum evolution in these open systems, we are developing analytical tools to solve quantum master equations using group-theoretical methods [3]. First applications include Floquet-PT systems [4] that show a strong reduction of the necessary loss for driving a PT-phase transition.
Integrated optical waveguides are highly suitable for implementing adiabatic quantum evolutions by generalizing STIRAP protocols for the evolution in degenerate dark subspaces. We have shown the first non-Abelian geometric quantum gate using an Abelian gauge field [5], and presented an optimal construction using the quantum metric. The concept of holonomic gates can be transferred to non-Hermitian systems [6] which becomes interesting in the framework of non-orthogonal waveguide modes. We also investigate highly degenerate structures for use in holonomic computation [7].
Rydberg physics with semiconductor excitons
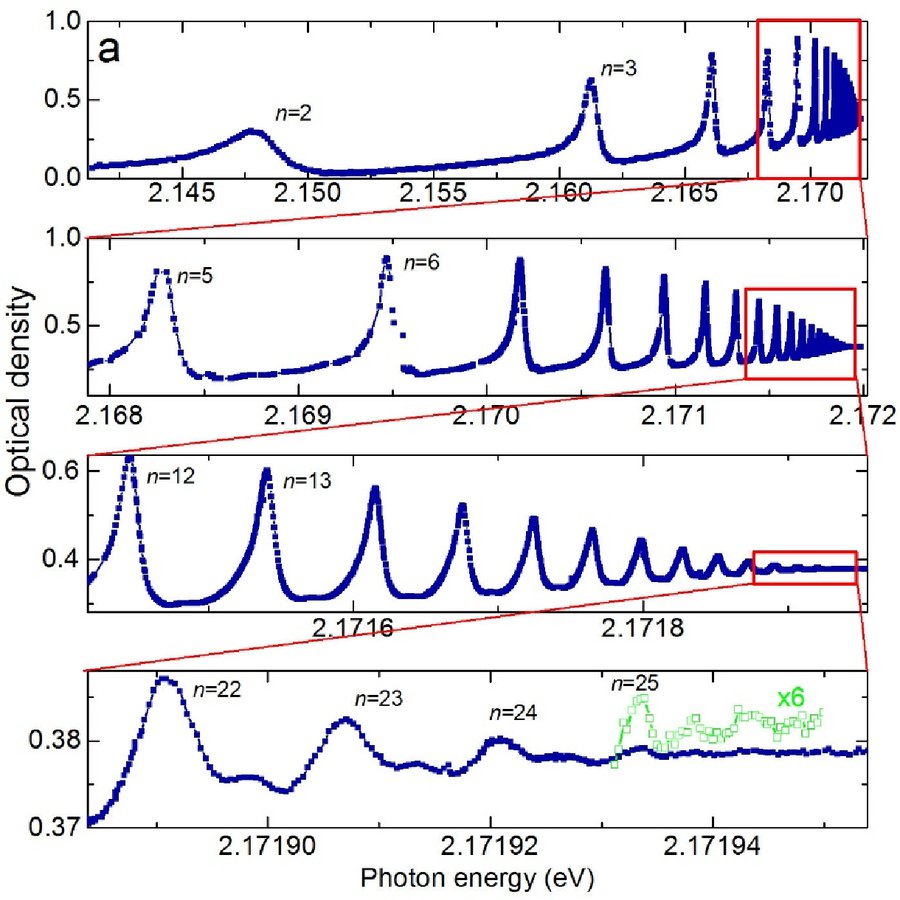
Rydberg atoms that have been excited to a quantum state with large principal quantum number n possess some extraordinary properties. For example, their exaggerated size, growing as n2, implies large dipole moments that also grow as n2 as well as dipole polarisabilities with an n7 scaling. Rydberg physics was so far limited to excitations in atomic systems. In collaboration with colleagues from the TU Dortmund, we have recently shown that Rydberg excitations can also be observed in semiconductor systems [1]. Here, the material in which the excitons were formed was a natural cuprous oxide (Cu2O) crystal. Rydberg excitons with principal quantum numbers up to n=25 have been observed in transmission spectroscopy (see Figure) which corresponds to an extension of the exciton wavefunction of more than one micrometer.
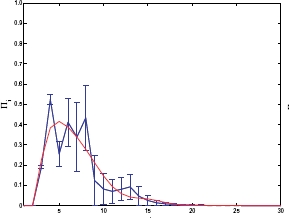
Similar to atoms, the binding energies of Rydberg excitons deviate systematically from the hydrogenic Rydberg series. This deviation can be cast into the form of a quantum defect which we showed to derive from the nonparabolicity of the valence bands [2,3]. We have shown further that the proximity of the Rydberg exciton resonances provides a route to detect coherent phenomena in semiconductor Rydberg excitons already in the absorption spectra [4]. There, additional resonances appear in the absorption spectrum that correspond to dressed states consisting of two Rydberg exciton levels coupled to the excitonic vacuum, forming a V-type three-level system, but driven only by one laser light source] (see Figure). Our result is based on the solution of the valence band Hamiltonian associated with the cubic crystal symmetry of Cu2O that corresponds to a modified Schrödinger equation in momentum space.
In crossed electric and magnetic fields, the potential landscape may be altered to provide additional quasi-bound states with giant dipoles [5], where we computed the eigenenergies of these giant-dipole excitons [6]. Stray electric fields on the other hand, such as those produced by charged impurities, leads to the vanishing of Rydberg resonances into an apparent continuum [7]. The appearance of additional absorption lines due to the broken rotational symmetry, together with spatially inhomogeneous Stark shifts, leads to a modification of the observed line shapes that agrees qualitatively with the changes observed in the experiment.
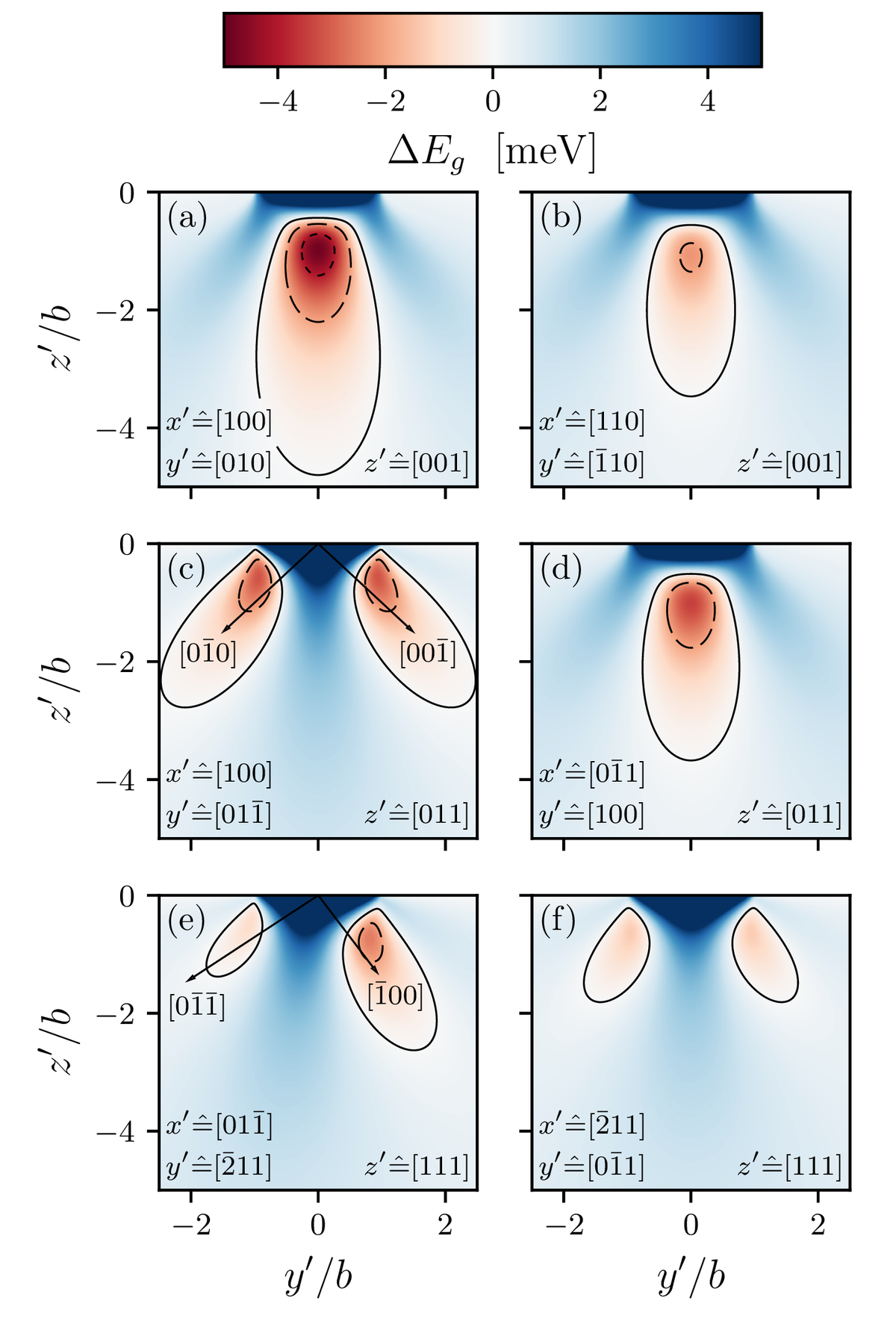
Additional potentials that modify the excitonic spectra include strain that could be used to trap Rydberg excitons [8] (see Figure).
Similar to atoms, dipole-dipole interactions dominate the overall interaction at the large distances relevant under experimental conditions of Rydberg exciton blockade. We have evaluated the long-range interactions between pairs of Rydberg excitons in Cu2O, which are due to direct Coulomb forces rather than short-range collisions typically considered for ground-state excitons [9], and found signatures of Rydberg blockade in pump-probe spectra [10]. For future experiments involving transitions between different exciton series in Cu2O, we have studied the infrared optical transitions between excitons of the yellow, green and blue series in Cu2O [11]. We showed that in many cases the dipole approximation is inadequate and, in particular, that it breaks down in yellow-blue transitions even for moderate principal quantum numbers.
For an introduction to Rydberg physics, we would like to refer you to Quantum Kate (en).
Machine learning methods for image reconstructions
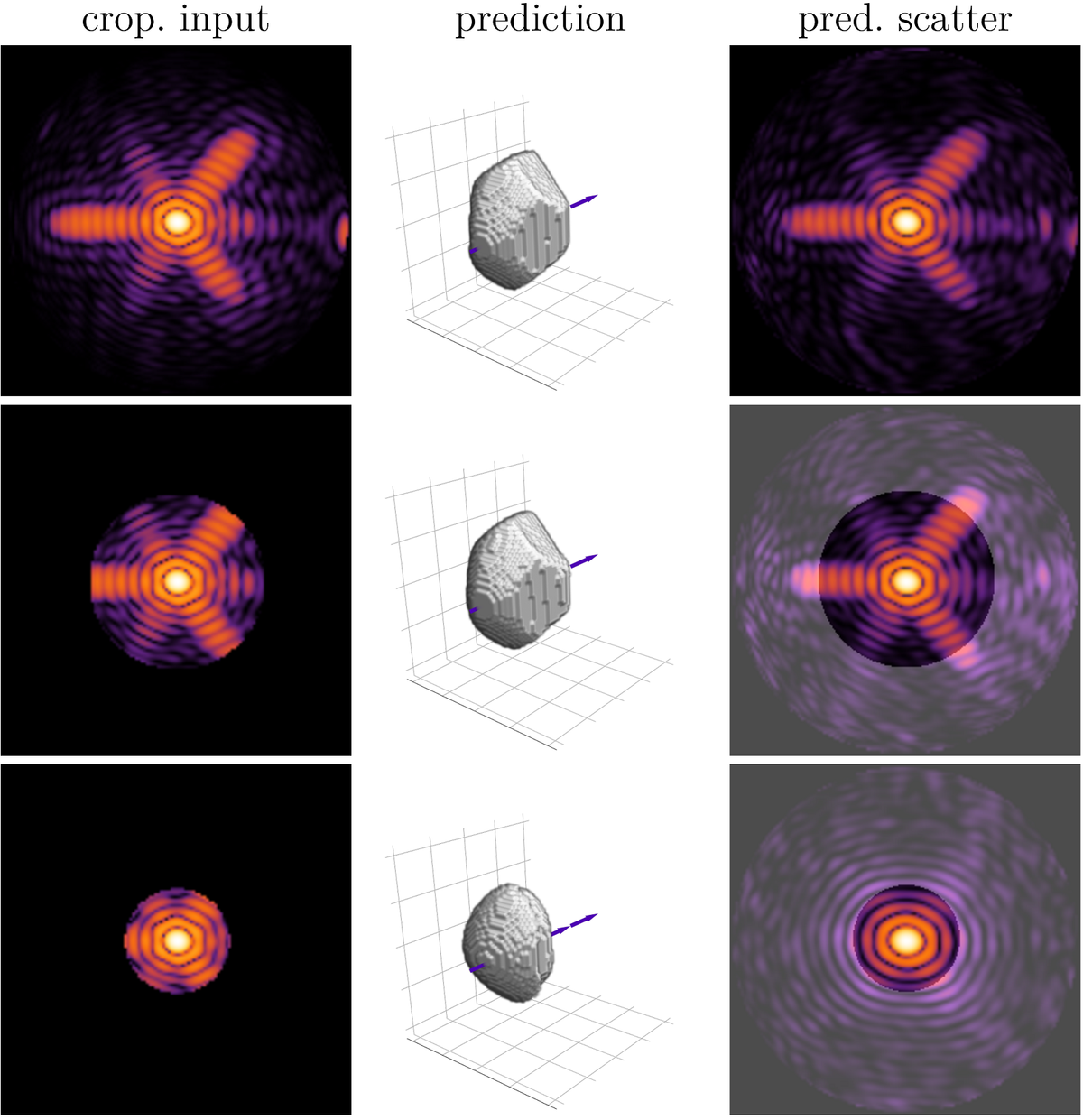
Single-shot x-ray imaging of short-lived nanostructures such as clusters and nanoparticles near a phase transition or non-crystalizing objects such as large proteins and viruses is currently the most elegant method for characterizing their structure. Wide-angle scattering using XUV or soft x-rays provides three-dimensional structural information in a single shot and has opened routes towards the characterization of non-reproducible objects in the gas phase. The retrieval of the structural information contained in wide-angle scattering images is highly non-trivial, and currently no efficient rigorous algorithm is known. We have shown that deep learning networks, trained with simulated scattering data, allow for fast and accurate reconstruction of shape and orientation of nanoparticles from experimental images [1]. The gain in speed compared to conventional retrieval techniques opens the route for automated structure reconstruction algorithms capable of real-time discrimination and pre-identification of nanostructures in scattering experiments with high repetition rate, thus representing the enabling technology for fast femtosecond nanocrystallography.
Recently, we have shown how a physics-informed deep neural network can be used to reconstruct complete three-dimensional object models on a voxel grid from single two-dimensional wide-angle scattering patterns [2]. We have demonstrated its universal reconstruction capabilities for silver nanoclusters, where the network uncovers novel geometric structures that reproduce the experimental scattering data with very high precision.
Dispersion forces
Dispersion forces such as Casimir forces between bodies, Casimir-Polder forces between atoms and bodies and van der Waals forces between atoms are effective electromagnetic forces that arise as consequences of correlated ground-state fluctuations. We are investigating dispersion forces in and out of thermal equilibrium [1,2,3] that are particularly relevant for long-wavelength atomic transitions as found in Rydberg atoms [4,5], and study universal scaling laws [6] and friction forces [7,8].
Dispersion forces occur in a variety of different contexts such as molecular interferometry where they influence the interference pattern of large molecules [9,10], and in diffraction processes of atom clouds off periodic surface potential landscapes [11]. Near nanofibers, we have shown that the Casimir-Polder force on an atom can be laterally tuned by choosing the appropriate atomic state for preparation [12], and the confinement of atoms inside a hollow-core fiber can be used to tune the van der Waals interaction between them [13].
QED in linear and nonlinear dielectric materials
One of the fundamental problems in understanding the interaction between light and dielectrics can be traced back to the question how to quantize the electromagnetic field in the presence of absorbing bodies. A consistent quantization scheme has been developed over the last 10 years or so which is based on a source-quantity representation of the electromagnetic field in terms of a bosonic vector field that describes collective excitations of field and absorbing matter [1,2]. In the linear-response approximation, this procedure is exact and has been used to treat atomic decoherence processes (spontaneous decay, dephasing, spatial decoherence etc.) as well dispersion forces (Casimir force, Casimir-Polder force) [3].
More recently, we have been able to extend this quantization scheme to include nonlinearly responding, absorbing dielectrics [4,5,6]. This enables us to study the effect of nonlinear absorption mechanisms in a quantum-mechanically consistent way. In the context of nonlocal or even nonreciprocal media, we have shown that the principle of macroscopic duality can still be upheld [7,8].
Quantum tomographic reconstruction with error bars
Verification of quantum states and processes requires a reconstruction of density matrices and CP maps that describes them. Together with K.M.R.Audenaert (Royal Holloway College) we are developing a novel quantum tomographic reconstruction method based on Bayesian inference via the Kalman filter update equations that also provides complete information about measurement uncertainties (error bars) [1]. This method allows also for a consistent treatment of imperfect photon detection [2].
Ultracold trapped neutral atoms, atom chips
With the advent of microfabricated structures (atom chips) that enable one to confine small numbers of neutral atoms near dielectric surfaces, we are able to study atom-surface interactions in great detail. The effects we investigate range from thermally induced spin flips [1] to spatial decoherence [2] and Casimir-Polder forces. More recently, we are beginning to understand effects of electromagnetic absorption in superconducting surfaces on coherence properties of atomic samples [3,4], and we will explore their potential use in high-precision measurements. Recently, we found evidence of directional spontaneous emission of atoms near a nanofiber [5].